Умножение чисел со старших разрядов в прямом коде

Пусть два числа X и Y представлены с фиксированной запятой в виде:

[X]пк = sign X.x1x2...xn – множимое [Y]пк = sign Y.y1y2...yn – множитель

Представим множитель в виде:

[Y]пк = sign Y. (y1*2-1 + y2*2-2 + ... + yn*2-n)

Тогда:

[Z]пк = [X]пк*[Y]пк = sign Z. |X| (y1*2-1 + y2*2-2 + ... + yn*2-n) = = sign Z. (|X|*y1*2-1 + |X|*y2*2-2 + ... + |X|*yn*2-n) = = sign Z. (|X|*2-1*y1 + |X|*2-2*y2 + ... + |X|*2-n*yn)

Это есть аналитическая запись алгоритма умножения двух чисел, начиная со старших разрядов множителя.

Алгоритм:

• Множимое сдвигается вправо на 1 разряд
• Анализируется цифра множителя. Если она – нуль, то частичное произведение не суммируется, а если она – единица, то частичное произведение добавляется к общему результату.
• Последовательность операций по пунктам 1 и 2 продолжается "n" раз.

• Знак произведения находится независимо от получения цифровой части по формуле:

  sign Z = sign X

  
  sign Y

Пример:

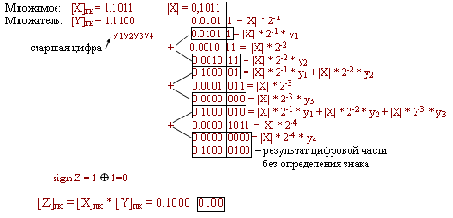
Видно, что в общем случае нужно иметь для точного результата сетку с числом разрядов, равным сумме разрядностей сеток сомножителей.

Если нужно получать произведение с точностью не хуже, чем 2-n, то достаточно иметь не удвоенную величину разрядной сетки, а лишь увеличенную на

d = log2n разрядов