Логические и арифметические основы и принципы работы ЭВМ
Умножение с младших разрядов в прямом коде
Напишем выражение для произведения двух чисел в несколько изменённом виде, а именно:
[Z]пк = [X]пк*[Y]пк = = sign Z.(|X|*y1*2-1 + |X|*y2*2-2 +... + |X|*yn*2-n ) = = sign Z.( |X|*2-1*y1 + 2-1 (|X|*2-1*y2 + 2-1 (|X|*2-1*y3 + (...)))) = = sign Z. ((...(( |X|*yn*2-1 + |X|*yn-1 )2-1 + |X|*yn-2 )2-1 + ... + + |X|*y2 )2-1 + |X|*y1 )*2-1
Это выражение называется преобразованием по схеме Горнера и задаёт алгоритм умножения с младших разрядов множителя.
Таким образом, для умножения должна выполняться следующая последовательность действий:
- Анализируется младшая цифра множителя. Если она равна "1", то множимое участвует в формировании части произведения. В противном случае – не участвует.
- Полученное частичное произведение сдвигается вправо на 1 разряд.
- Операции по пунктам 1 и 2 выполняются до старшего разряда.
Пример:
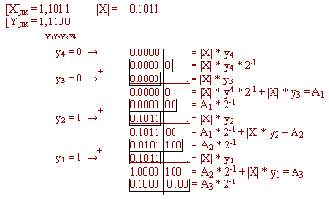
signZ= 1
