Основные положения машины Тьюринга

1. Машина Тьюринга (рис.10.1) имеет конечное число знаков si, образующих внешний алфавит, в котором кодируются сведения, подаваемые в МТ, а также вырабатываемые в ней. Среди знаков имеется пустой знак (s1), посылка которого в какую-либо ячейку стирает находившийся в ней знак и оставляет ее пустой.

   
   
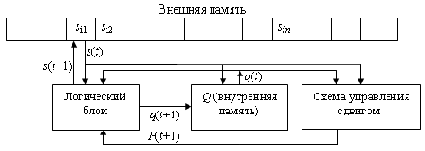
   Рис. 10.1.  Структура машины Тьюринга

   В зависимости от поданной начальной информации

   
   (содержащихся на ленте внешней памяти знаков) возможны два случая:
   • после конечного числа тактов машина останавливается (имея информацию ?), подавая сигнал об остановке. В этом случае МТ применима к информации
     
     и перерабатывает ее в информацию ?;
   • остановка никогда не наступает. В этом случае МТ не применима к начальной информации
     
     .

2. В каждый момент обозревается лишь одна ячейка ленты (памяти). Переход может осуществляться лишь к соседней ячейке ( R – вправо, L–влево, N– нет перехода (остаться)). Переход к произвольной ячейке производится путем последовательного перебора всех ячеек, разделяющих текущую и необходимую ячейки. На каждом отдельном такте t команда предписывает только замену единственного знака si, хранящегося в обозреваемой ячейке, каким-либо другим знаком sj.

3. Логический блок МТ имеет конечное число состояний {qi} i=1..m.

   Знаки R, L, N, q1,..,qmобразуют внутренний алфавит машины.

   Переработанный знак sj, записываемый в просматриваемую ячейку, состояние, которое примет машина Тьюринга в следующем такте q(t+1) и выполняемая в данном такте операция перехода к следующей ячейке P(t+1) являются функцией анализируемого в данном такте символа и текущего состояния машины si и q(t):

   si(t+1)=f1(si,q(t)); q(t+1)=f2(si,q(t)); P(t+1)=f3(si,q(t)).

   Программа для МТ определяется тройкой {si, P, q}t.

   Пример записи программы вычисления логической функции "неравнозначность" для машины Тьюринга представлен ниже.

   Символ (si)Состояниеq1q2q3q4

   0	0, R, q2	0, N, q4	1, N, q4	0, N, q4
   1	1, R, q3	1, N, q4	0, N, q4	1, N, q4

   Перед началом работы машина Тьюринга находится в состоянии q1 считывания первого операнда.

   Данная МТ применима к исходной информации. Останов – состояние q4. Значение si в ячейке y не меняется (сохраняется результат).

   Если программа для МТ будет определена таблицей переходов

   Символ (si)Состояниеq1q2q3q4

   0	0, R, q2	0, N, q4	1, N, q4	1, N, q4
   1	1, R, q3	1, N, q4	0, N, q4	0, N, q4

   то данная МТ будет не применима к исходной информации, поскольку в состоянии q4 значение si в ячейке y постоянно меняется на противоположное.