Порядок проектирования комбинационных схем

При проектировании схем, выполняющих ту или иную логическую функцию, необходимо обеспечить минимизацию аппаратных затрат на реализацию этих схем, а также во многих случаях необходимо сократить номенклатуру используемых логических элементов. Последнее требование реализуется путем выбора соответствующей системы элементов. В настоящее время основные серии интегральных логических схем включают в себя элементы, составляющие некоторый функционально полный логический базис, а также дополнительные элементы, реализующие часто встречающиеся логические функции [1]. В качестве функционально полных базисов используются, как правило, одноэлементные базисы "И-НЕ" либо "ИЛИ-НЕ".

Рассмотрим этапы проектирования комбинационных логических схем на одноэлементном базисе "И-НЕ" без использования каких-либо дополнительных логических элементов на примере проектирования одноразрядного комбинационного сумматора. Такой сумматор является основой построения многоразрядной суммирующей схемы, выполняющей операции над числами, представленными в том или ином коде.

Пример выполнения операции суммирования чисел, представленных в обратном коде:

Xок=0.1011

Yок=1.0110

+0.1011

1.0110

+1.0.0001

_______1

0.0010

Из примера видно, что в каждом разряде происходит суммирование соответствующих разрядов операндов и переноса, поступающего из предыдущего разряда (для младшего разряда – циклический перенос из знакового разряда). При этом вырабатывается значение суммы в этом разряде и перенос в следующий разряд.

Условно-графическое обозначение элемента, выполняющего эти действия, приведено на рис. 13.4.

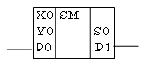
Рис. 13.4.  Условно-графическое обозначение одноразрядого сумматора

Рассмотрим основные этапы проектирования такой схемы.

Этап 1. Представление функции, выполняемой проектируемой схемой, в каноническом виде, то есть в виде таблицы истинности или одной из совершенных нормальных форм записи. Обычно на этом этапе функцию легче описать таблицей истинности. Так как проектируется двухвыходная логическая схема, то необходимо представить таблицу истинности для каждого ее выхода (табл. 13.6).

Таблица 13.6. ВходыВыходыXiYiPiSiPi+1

0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

Этап 2. Минимизация логической функции. На этом этапе можно использовать любые методы минимизации [5]. Специфика минимизации многовыходных функций – необходимость получения устройства, имеющего минимальный общий состав оборудования, то есть следует проводить минимизацию одной функции с учетом возможного использования части полученного оборудования для минимизации другой функции. В нашем примере не будем рассматривать эту особенность и проведем автономную минимизацию каждой функции. Минимизацию логических функций можно проводить различными методами: методом Квайна, его модификацией – методом Квайна – Мак-Класки, методом диаграмм Вейча. Метод диаграмм Вейча удобно использовать для минимизации функций от небольшого (до четырех) числа переменных. Диаграмма Вейча для функции Si представлена в табл. 13.7.

Таблица 13.7. Диаграмма Вейча для функции суммы одноразрядного сумматора

	yi		yi
xi	0	1	0	1
xi	1	0	1	0
	pi	pi		pi

Из диаграммы видно, что минимальная дизъюнктивная нормальная форма для функции суммы одноразрядного сумматора совпадает с ее совершенной дизъюнктивной нормальной формой:

Si= xiyi pi xi yipi xiyipi xiyipi

Диаграмма Вейча для функции Pi+1 представлена в табл. 13.8.

Таблица 13.8. Диаграмма Вейча для функции переноса одноразрядного сумматора

	yi		yi
xi	1	1	1	0
xi	0	1	0	0
	pi	pi		pi

Минимальная дизъюнктивная нормальная форма для этой функции имеет вид:

Рi+1= xiyi xipi yipi

Этап 3. Перевод функции в базис, в котором будет строиться схема. В выбранном варианте это базис "Штрих Шеффера":


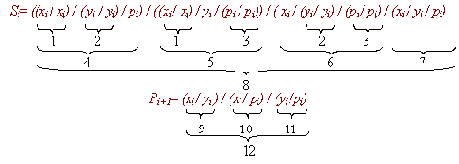
Рис. . 

Этап 4. Составление схемы на элементах, реализующих функции выбранного базиса. Для более наглядного отображения этого этапа выше обозначены номера элементов, которые будут реализовывать ту или иную часть функции. Полученные схемы представлены на рис.13.5 и 13.6.


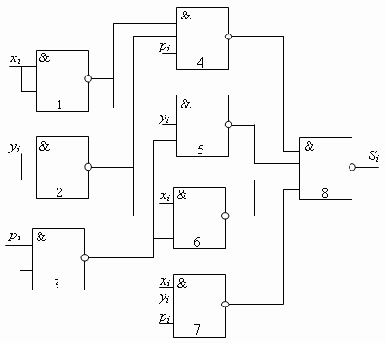
Рис. 13.5.  Схема, реализующая функцию суммы одноразрядного сумматора


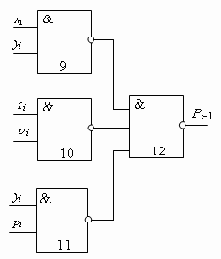
Рис. 13.6.  Схема, реализующая функцию переноса одноразрядного сумматора


Содержание раздела

---

---